Эта статья о том, как вычислить неберущийся интеграл онлайн, содержит примеры вычисления неберущихся интегралов с помощью Вольфрам Альфа.
Здесь продолжена тема, которая рассматривалась в статьях Определенный интеграл в Wolfram|Alpha, Как вычислить приближенное значение определенного интеграла в Wolfram|Alpha, используя численные методы решения интегралов, Численное интегрирование в Wolfram|Alpha, и рассмотрены основные способы вычисления неберущихся интегралов в системе Вольфрам Альфа.
Вычислить интеграл - так говорят об определенном интеграле, поскольку определенный интеграл, по его определению, есть число, которое "вычисляется", в отличие от неопределенного интеграла, который есть переменная величина, и поэтому "находится".
Что же такое "неберущийся" интеграл? Так называют неопределенные интегралы, которые не выражаются через элементарные функции. То есть, это интегралы, в которых первообразную подынтегральной функции нельзя найти легко и быстро. Найти-то ее в принципе можно, но лень. Или же не хватает времени, знаний... Тогда и говорят, что первообразная не существует, и интеграл неберущийся.
Определенные интегралы также называют неберущимися, когда определенный интеграл существует, как предел интегральной суммы, но подынтегральная функция не имеет первообразной, либо когда первообразная подынтегральной функции не выражается через элементарные функции.
Таким образом, различают, когда определенный интеграл, как предел интегральной суммы, в принципе существует, но "не берется", и когда определенный интеграл не существует в принципе. Примеры можно также найти в статье Несобственные интегралы в Wolfram|Alpha.
Вот простой пример неберущегося интеграла:
integrate e^(x^2), x=0..1
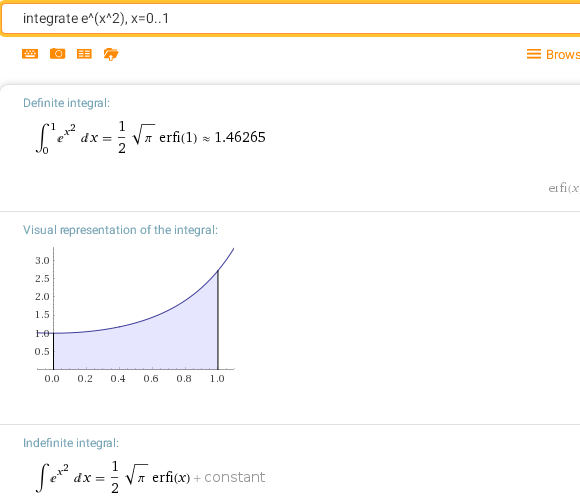
Как видим, этот интеграл существует, но выражается через неэлементарную функцию erfi(x), которая является мнимой частью функции ошибок erf(ix).
Второй типичный пример:
integrate e^(-x^2), x=0..1

Здесь erf(x) - функция ошибок (интеграл вероятностей), неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных.
Другие типичные примеры неберущихся интегралов, которые находят применение в физике, точнее, в оптике:
integrate sin(x^2), x=0..1
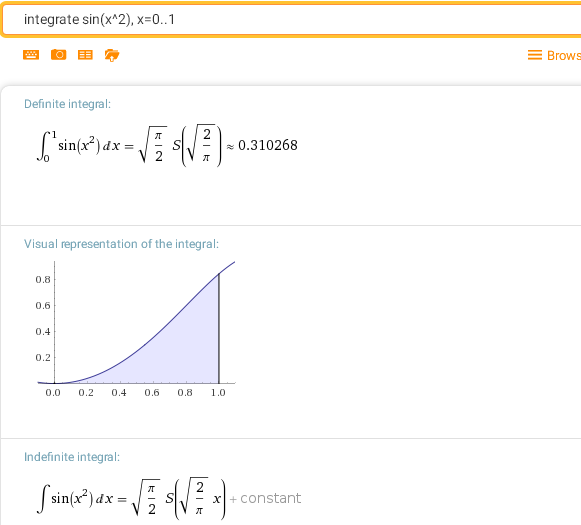
Этот интеграл также выражается через неэлементарную функцию S(x), которая называется S-интеграл Френеля.
integrate cos(x^2), x=0..1
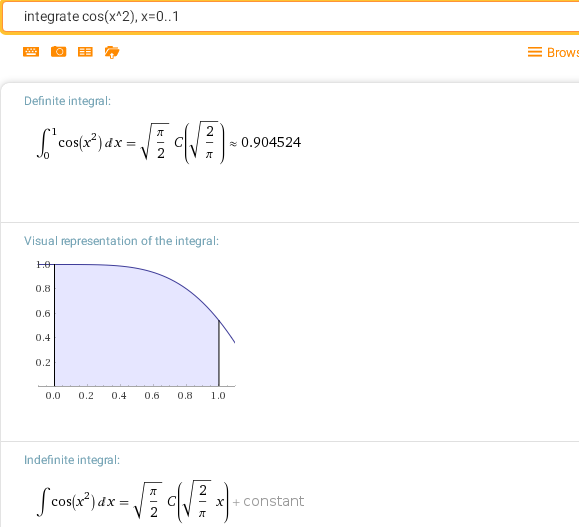
Этот интеграл, также выражается через неэлементарную функцию C(x), которая называется C-интеграл Френеля (Fresnel C integral).
На самом деле, эти, как и некоторые другие неэлементарные функции, определяются через соответствующие интегралы.
Например, S-интеграл Френеля (Fresnel S integral) и C-интеграл Френеля (Fresnel C integral) определяются следующим образом
integrate sin(pi*t^2/2) dt, t= 0..x - S-интеграл Френеля
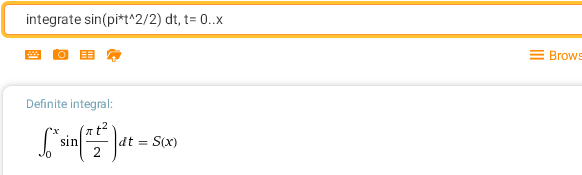
integrate cos(pi*t^2/2) dt, t= 0..x - C-интеграл Френеля
integrate -cos(t)/t, t= x..inf - интегральный косинус

integrate sin(t)/t, t= 0..x - интегральный синус
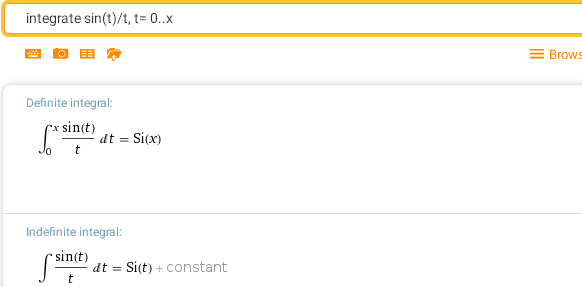

Соответственно, через эти функции выражаются такие интегралы, как


Вольфрам Альфа - интеллектуальная система, которая в большинстве случаев правильно реагирует даже на запросы, составленные неправильно с точки зрения строгой математики. Например, следующие варианты запроса на вычисление определенного интеграла дают одинаковый результат.
integrate sqrt(1-sin^2(x)/4), x=0..pi
integrate sqrt(1-(sinx)^2/4), x=0..pi
integrate sqrt(1-sinx^2/4), x=0..pi
integrate sqrt(1-sin^2x/4), x=0..pi
integrate sqrt(1-sin^2(x)/4), x=0..pi
integrate sqrt(1-sin(x)^2/4), x=0..pi

Однако, из правила всеядности Вольфрам Альфа существуют исключения. Вот почему, когда используете Вольфрам Альфа, все же лучше строго соблюдать правила математической нотации. Например,
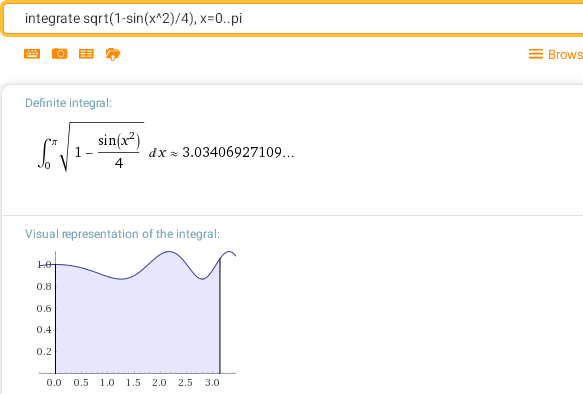
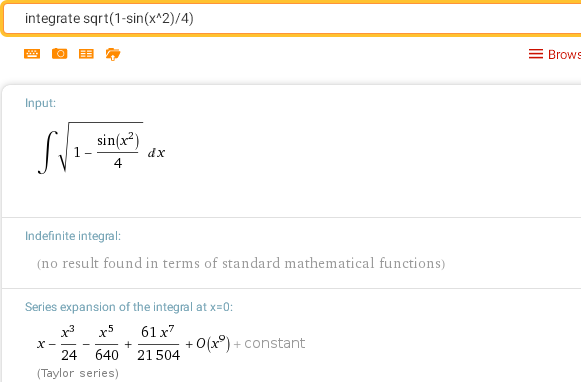
Кстати, этот последний интеграл, который, как и предыдущие, тоже является "неберущимся". Но при этом он не выражается даже через неэлементарные функции. В этом легко убедится непосредственно, найдя неопределенный интеграл, который, как видим, представляется в виде степенного ряда:
integrate sqrt(1-sin(x^2)/4)
Отметим, что определенный интеграл может быть не только действительным, но также комплексным или мнимым числом:
integrate sqrt(1-e^(x^2)), x=0..pi


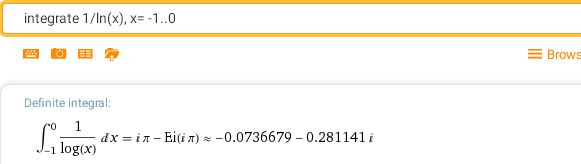
В последнем примере для вычисления интеграла используется еще одна неэлементарная функция, на этот раз Ei(x).
Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.
Посетите страницу Как поддержать наш сайт?
Здесь продолжена тема, которая рассматривалась в статьях Определенный интеграл в Wolfram|Alpha, Как вычислить приближенное значение определенного интеграла в Wolfram|Alpha, используя численные методы решения интегралов, Численное интегрирование в Wolfram|Alpha, и рассмотрены основные способы вычисления неберущихся интегралов в системе Вольфрам Альфа.
Вычислить интеграл - так говорят об определенном интеграле, поскольку определенный интеграл, по его определению, есть число, которое "вычисляется", в отличие от неопределенного интеграла, который есть переменная величина, и поэтому "находится".
Что же такое "неберущийся" интеграл? Так называют неопределенные интегралы, которые не выражаются через элементарные функции. То есть, это интегралы, в которых первообразную подынтегральной функции нельзя найти легко и быстро. Найти-то ее в принципе можно, но лень. Или же не хватает времени, знаний... Тогда и говорят, что первообразная не существует, и интеграл неберущийся.
Определенные интегралы также называют неберущимися, когда определенный интеграл существует, как предел интегральной суммы, но подынтегральная функция не имеет первообразной, либо когда первообразная подынтегральной функции не выражается через элементарные функции.
Таким образом, различают, когда определенный интеграл, как предел интегральной суммы, в принципе существует, но "не берется", и когда определенный интеграл не существует в принципе. Примеры можно также найти в статье Несобственные интегралы в Wolfram|Alpha.
Вот простой пример неберущегося интеграла:
integrate e^(x^2), x=0..1

Как видим, этот интеграл существует, но выражается через неэлементарную функцию erfi(x), которая является мнимой частью функции ошибок erf(ix).
Второй типичный пример:
integrate e^(-x^2), x=0..1

Здесь erf(x) - функция ошибок (интеграл вероятностей), неэлементарная функция, возникающая в теории вероятностей, статистике и теории дифференциальных уравнений в частных производных.
Другие типичные примеры неберущихся интегралов, которые находят применение в физике, точнее, в оптике:
integrate sin(x^2), x=0..1

Этот интеграл также выражается через неэлементарную функцию S(x), которая называется S-интеграл Френеля.
integrate cos(x^2), x=0..1

Этот интеграл, также выражается через неэлементарную функцию C(x), которая называется C-интеграл Френеля (Fresnel C integral).
На самом деле, эти, как и некоторые другие неэлементарные функции, определяются через соответствующие интегралы.
Например, S-интеграл Френеля (Fresnel S integral) и C-интеграл Френеля (Fresnel C integral) определяются следующим образом
integrate sin(pi*t^2/2) dt, t= 0..x - S-интеграл Френеля

integrate cos(pi*t^2/2) dt, t= 0..x - C-интеграл Френеля
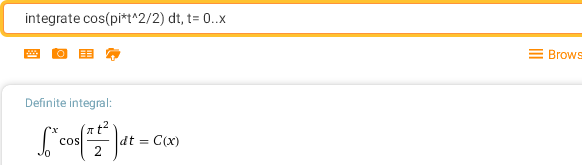 |
К таким же не элементарным функциям относятся Ci(x) - интегральный косинус, Si(x) - интегральный синус, li(x) - интегральный логарифм, соответственно:
integrate -cos(t)/t, t= x..inf - интегральный косинус

integrate sin(t)/t, t= 0..x - интегральный синус

integrate 1/ln(t), t= 0..x - интегральный логарифм

Соответственно, через эти функции выражаются такие интегралы, как


Вольфрам Альфа - интеллектуальная система, которая в большинстве случаев правильно реагирует даже на запросы, составленные неправильно с точки зрения строгой математики. Например, следующие варианты запроса на вычисление определенного интеграла дают одинаковый результат.
integrate sqrt(1-sin^2(x)/4), x=0..pi
integrate sqrt(1-(sinx)^2/4), x=0..pi
integrate sqrt(1-sinx^2/4), x=0..pi
integrate sqrt(1-sin^2x/4), x=0..pi
integrate sqrt(1-sin^2(x)/4), x=0..pi
integrate sqrt(1-sin(x)^2/4), x=0..pi

Последний интеграл также неберущийся. Он выражается через эллиптический интеграл второго рода E(x).
Однако, из правила всеядности Вольфрам Альфа существуют исключения. Вот почему, когда используете Вольфрам Альфа, все же лучше строго соблюдать правила математической нотации. Например,

Кстати, этот последний интеграл, который, как и предыдущие, тоже является "неберущимся". Но при этом он не выражается даже через неэлементарные функции. В этом легко убедится непосредственно, найдя неопределенный интеграл, который, как видим, представляется в виде степенного ряда:
integrate sqrt(1-sin(x^2)/4)

Отметим, что определенный интеграл может быть не только действительным, но также комплексным или мнимым числом:
integrate sqrt(1-e^(x^2)), x=0..pi



В последнем примере для вычисления интеграла используется еще одна неэлементарная функция, на этот раз Ei(x).
Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.
Посетите страницу Как поддержать наш сайт?