Очередной канун Нового Года... морозная погода и снежинки на оконном стекле... Все это побудило меня вновь написать о... фракталах, и о том, что знает об этом Вольфрам Альфа. По этому поводу есть интересная статья Математические снежинки в Wolfram|Alpha, в которой имеются примеры двумерных фрактальных структур. Здесь же мы рассмотрим более сложные примеры трехмерных фракталов.
Кроме внешней привлекательности, губка Менгера имеет очень интересные и неожиданные свойства, о которых стоит упомянуть отдельно.
Например, если количество итераций при построении данного фрактала по указанному выше правилу, равно 0, мы получаем геометрический объект, площадь поверхности которого равна 6, а его объем равен 1 или 100% от объема исходного тела:
menger sponge, iterations=0

При количестве итераций равном 1, получим губку Менгера с площадью поверхности 8, и объемом 20/27 (примерно 0,74 или 74% от исходного объема):
menger sponge, iterations=1

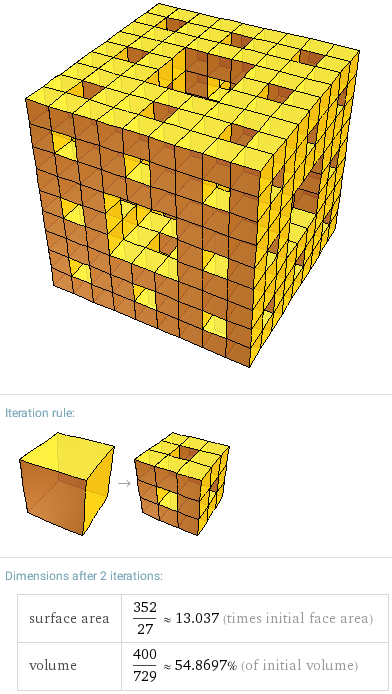
Соответственно, при количестве итераций равном 2, получаем объект, показанный вначале этой статьи, с площадью поверхности 352/27 и объемом 400/729 (примерно 55% от исходного):
menger sponge, iterations=2
Если рассмотреть бесконечную последовательность значений площади поверхности и объема губки Менгера, то в пределе площадь поверхности этого фрактала стремится к бесконечности, а в его объем стремится к нулю. В этом заключается одно из самых удивительных свойств губки Менгера. При этом значение ее фрактальной размерности (capacity dimention) стремится к отношению ln(20)/ln(3):

Ортогональные проекции губки Менгера, представляют собой двумерный фрактал - ковер Серпинского:

Фрактал можно наглядно представить (описать), как геометрическую фигуру или тело (имея ввиду, что и то и другое есть множество, в данном случае, множество точек), детали которой имеют такую же форму, как и сама исходная фигура. То есть, это самоподобная структура, рассматривая детали которой при увеличении, мы будем видеть ту же самую форму, что и без увеличения. Тогда как в случае обычной геометрической фигуры (не фрактала), при увеличении мы увидим детали, которые имеют более простую форму, чем сама исходная фигура. Например, при достаточно большом увеличении часть эллипса выглядит, как отрезок прямой. С фракталами такого не происходит: при любом их увеличении мы снова увидим ту же самую сложную форму, которая с каждым увеличением будет повторяться снова и снова.
 |
| Benoit Mandelbrot (1924-2010) |
Бенуа Мандельброт (Benoit Mandelbrot), основоположник науки о фракталах, в своей статье Фракталы и искусство во имя науки написал: "Фракталы - это геометрические формы, которые в равной степени сложны в своих деталях, как и в своей общей форме. То есть, если часть фрактала будет увеличена до размера целого, она будет выглядеть, как целое, или в точности, или, возможно, с небольшой деформацией".
Губка Менгера - один из самых известных и популярных трехмерных фракталов. Ее автором является математик Карл Менгер (Karl Menger, 1902-1985).
Любой фрактал строится по определенному правилу, которое последовательно применяется неограниченное количество раз. Каждый такой раз называется итерацией.
 |
| Menger sponge, губка Менгера |
Итеративный алгоритм построения губки Менгера достаточно простой: исходный куб со стороной 1 делится плоскостями, параллельными его граням, на 27 равных кубов. Из него удаляются один центральный куб и 6 прилежащих к нему по граням кубов. Получается множество, состоящее из 20 оставшихся меньших кубов. Поступая так же с каждым из этих кубов, получим множество, состоящее уже из 400 меньших кубов. Продолжая этот процесс бесконечно, получим губку Менгера.
Губка Менгера стала широко известной, не только потому, что имеет характерную форму, которая дарит эстетическое наслаждение от ее созерцания. Динамику популярности этого трехмерного фрактала по всему миру в реальном времени показывает график Google Trands (дождитесь загрузки данных):
Губка Менгера стала широко известной, не только потому, что имеет характерную форму, которая дарит эстетическое наслаждение от ее созерцания. Динамику популярности этого трехмерного фрактала по всему миру в реальном времени показывает график Google Trands (дождитесь загрузки данных):
Кроме внешней привлекательности, губка Менгера имеет очень интересные и неожиданные свойства, о которых стоит упомянуть отдельно.
Например, если количество итераций при построении данного фрактала по указанному выше правилу, равно 0, мы получаем геометрический объект, площадь поверхности которого равна 6, а его объем равен 1 или 100% от объема исходного тела:
menger sponge, iterations=0

При количестве итераций равном 1, получим губку Менгера с площадью поверхности 8, и объемом 20/27 (примерно 0,74 или 74% от исходного объема):
menger sponge, iterations=1

Соответственно, при количестве итераций равном 2, получаем объект, показанный вначале этой статьи, с площадью поверхности 352/27 и объемом 400/729 (примерно 55% от исходного):
menger sponge, iterations=2

Если рассмотреть бесконечную последовательность значений площади поверхности и объема губки Менгера, то в пределе площадь поверхности этого фрактала стремится к бесконечности, а в его объем стремится к нулю. В этом заключается одно из самых удивительных свойств губки Менгера. При этом значение ее фрактальной размерности (capacity dimention) стремится к отношению ln(20)/ln(3):

Ортогональные проекции губки Менгера, представляют собой двумерный фрактал - ковер Серпинского:

Обратите внимание на свойства этого фрактала, которые вы теперь можете прочитать и изучить самостоятельно.
Также Вольфрам Альфа предлагает всем, кого интересуют эксперименты с фракталами, мобильное приложение Wolfram Fractals Reference App, которое можно загрузить через iTunes или Gogle Play со станицы Fractals Reference App.
Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.
Посетите страницу Как поддержать наш сайт?
В заключение, еще один пример известного трехмерного фрактала - тетраэдр Серпинского (Sierpinski tetrahedron). По данным Google Trands, популярность тетраэдра Серпинского по каким-то причинам уступает популярности губки Менгера:
Также Вольфрам Альфа предлагает всем, кого интересуют эксперименты с фракталами, мобильное приложение Wolfram Fractals Reference App, которое можно загрузить через iTunes или Gogle Play со станицы Fractals Reference App.
Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.
Посетите страницу Как поддержать наш сайт?
