Запрос solve, который был использован ранее, чтобы получить решение системы линейных алгебраических уравнений (СЛАР) в Wolfram|Alpha, на самом деле является универсальным запросом для решения уравнений и их систем в Wolfram|Alpha. Собственно для решения системы линейных алгебраических уравнений он применяется лишь тогда, когда эта система задана в естественном виде: после запроса solve все уравнения системы перечисляются через запятую. Этот способ хорош тем, что позволяет решать не только определенные, но также и неопределенные системы - в общем виде.
Для решения определенных систем линейных алгебраических уравнений применяется также матричный способ.
В Wolfram|Alpha для решения систем линейных алгебраических уравнений матричным способом служит специальный запрос LinearSolve, после которого указываем матрицу коэффициентов системы и вектор (матрицу-столбец) свободных членов.
Чтобы понять особенности синтаксиса запроса LinearSolve, изучите следующие примеры.
Для начала рассмотрим решение однородных систем линейных алгебраических уравнений. После запроса LinearSolve вводим матрицу коэффициентов системы и нулевой вектор свободных членов. Получаем:
LinearSolve[{{a, b}, {c, d}}, {0, 0}]
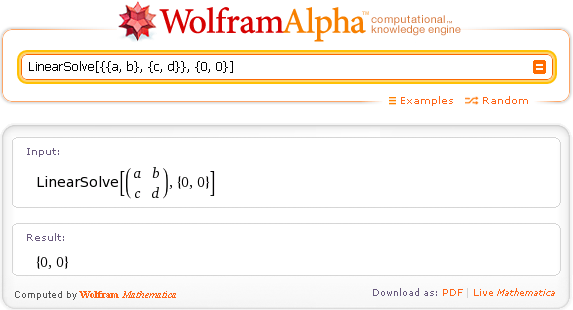
Здесь Wolfram|Alpha дает тривиальное решение {0, 0}.
Точно также легко Wolfram|Alpha выводит тривиальное решение и для однородных систем линейных алгебраических уравнений более высокой размерности.
LinearSolve[{{1, 1, 1, -1}, {2, 1, 1, -2}, {1, 1, 2, 1}, {1, 1, 2, 4}}, {0, 0, 0, 0}]

Теперь взглянем на решение неоднородных систем линейных алгебраических уравнений.
После запроса LinearSolve вводим матрицу коэффициентов системы и ненулевой вектор свободных членов. В ответ получаем вектор неизвестных. Вот два примера.
LinearSolve[{{a, b}, {c, d}}, {1, 2}]

LinearSolve[{{1, 1, 1, -1}, {2, 1, 1, -2}, {1, 1, 2, 1}, {1, 1, 2, 4}}, {1, 1, 1, 2}]

Для решения определенных систем линейных алгебраических уравнений применяется также матричный способ.
В Wolfram|Alpha для решения систем линейных алгебраических уравнений матричным способом служит специальный запрос LinearSolve, после которого указываем матрицу коэффициентов системы и вектор (матрицу-столбец) свободных членов.
Чтобы понять особенности синтаксиса запроса LinearSolve, изучите следующие примеры.
Для начала рассмотрим решение однородных систем линейных алгебраических уравнений. После запроса LinearSolve вводим матрицу коэффициентов системы и нулевой вектор свободных членов. Получаем:
LinearSolve[{{a, b}, {c, d}}, {0, 0}]

Здесь Wolfram|Alpha дает тривиальное решение {0, 0}.
Точно также легко Wolfram|Alpha выводит тривиальное решение и для однородных систем линейных алгебраических уравнений более высокой размерности.
LinearSolve[{{1, 1, 1, -1}, {2, 1, 1, -2}, {1, 1, 2, 1}, {1, 1, 2, 4}}, {0, 0, 0, 0}]

Теперь взглянем на решение неоднородных систем линейных алгебраических уравнений.
После запроса LinearSolve вводим матрицу коэффициентов системы и ненулевой вектор свободных членов. В ответ получаем вектор неизвестных. Вот два примера.
LinearSolve[{{a, b}, {c, d}}, {1, 2}]

LinearSolve[{{1, 1, 1, -1}, {2, 1, 1, -2}, {1, 1, 2, 1}, {1, 1, 2, 4}}, {1, 1, 1, 2}]
