Для поиска аналитических решений обыкновенных дифференциальных уравнений Wolfram Alpha использует стандартный запрос solve (см. Решение обыкновенных дифференциальных уравнений в Wolfram Alpha). Если же аналитическое решение дифференциального уравнения найти невозможно, этот запрос выводит лишь семейство интегральных кривых данного уравнения. Например,




Очевидно, для получения таких интегральных кривых система Wolfram|Alpha использует приближенные (численные) методы интегрирования дифференциальных уравнений.
Чтобы получить само численное решение обыкновенного дифференциального уравнения (Ordinary Differential Equation, ODE, Numerical Differential Equation Solving), в частности, в виде таблицы значений искомой функции, запрос solve нужно уточнить, дополнив его специальными параметрами:
solve {дифференциальное уравнение, начальные условия} (метод интегрирования) [шаг интегрирования] [отрезок интегрирования]
Обязательные параметры - само дифференциальное уравнение, начальные условия и численный метод интегрирования.
Не забудьте, что количество начальных условий должно совпадать с порядком уравнения. Иначе, Wolfram Alpha автоматически подставит в запрос свои начальные или краевые условия.
Рекомендуется указывать явно отрезок интегрирования. Без этого Wolfram Alpha автоматически выполнит 10 шагов интегрирования по умолчанию. Можно явно указать шаг интегрирования. В противном случае, Wolfram Alpha установит шаг интегрирования по умолчанию, как в следующем примере:
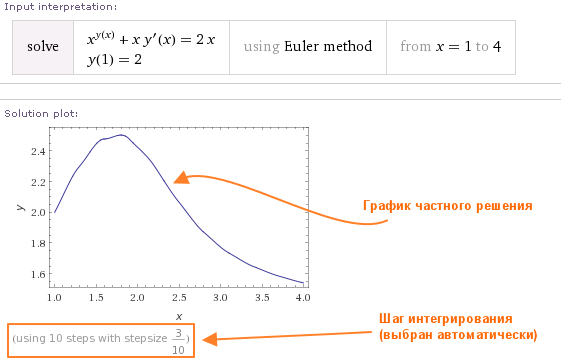
Если указаны все необходимые параметры, то кроме графика численного решения дифференциального уравнения (интегральной кривой), Wolfram Alpha также выведет само численное решение - таблицу значений искомой функции:

Когда дифференциальное уравнение, которое вы решаете численным методом, допускает также аналитическое решение, тогда по запросу solve система Wolfram Alpha выводит точную и приближенную интегральные кривые уравнения, соответствующие заданным начальным условиям, а также график погрешностей, таблицу значений искомой функции, таблицу погрешностей, и, конечно, само аналитическое решение:

Кроме того, здесь Wolfram Alpha выводит таблицу для сравнения погрешностей всех численных методов, которые использует система (в крайней точке интервала интегрирования дифференциального уравнения):

В рассмотренном примере шаг интегрирования, равный 0.2, был выбран автоматически. Выше было сказано, что можно явно указать нужный шаг интегрирования. Причем, нужно выбирать его так, чтобы на заданном отрезке умещалось не менее, чем 10 шагов интегрирования. Уменьшая шаг интегрирования, можно получать численные решения с желаемой точностью точностью:
solve {y'+2xy=0, y(1)=2} Euler method h=.05 x=1..3

Численные решения дифференциальных уравнений, рассмотренные выше, были получены простейшим методом - методом Эйлера (Euler method). Как мы видели выше, Wolfram Alpha реализует и другие численные методы интегрирования дифференциальных уравнений. Посмотрите примеры (по ссылке):
С помощью Wolfram Alpha, можно решать не только обыкновенные дифференциальные уравнения 1-го порядка (ОДУ-1), но и обыкновенные дифференциальные уравнения высших порядков. Например, вот так Wolfram Alpha решает обыкновенное дифференциальное уравнение 3-го порядка:
solve {y```= -2xy`, y(0) = 0, y`(0) = -1, y``(0) = -2} Runge-Kutta method h =.25 x=0..3

Таким образом, численное решение обыкновенных дифференциальных уравнений в системе Wolfram Alpha является достаточно простой стандартной процедурой, соблюдение которой гарантирует правильный результат.
solve {дифференциальное уравнение, начальные условия} (метод интегрирования) [шаг интегрирования] [отрезок интегрирования]
Обязательные параметры - само дифференциальное уравнение, начальные условия и численный метод интегрирования.
Не забудьте, что количество начальных условий должно совпадать с порядком уравнения. Иначе, Wolfram Alpha автоматически подставит в запрос свои начальные или краевые условия.
Рекомендуется указывать явно отрезок интегрирования. Без этого Wolfram Alpha автоматически выполнит 10 шагов интегрирования по умолчанию. Можно явно указать шаг интегрирования. В противном случае, Wolfram Alpha установит шаг интегрирования по умолчанию, как в следующем примере:


Когда дифференциальное уравнение, которое вы решаете численным методом, допускает также аналитическое решение, тогда по запросу solve система Wolfram Alpha выводит точную и приближенную интегральные кривые уравнения, соответствующие заданным начальным условиям, а также график погрешностей, таблицу значений искомой функции, таблицу погрешностей, и, конечно, само аналитическое решение:

Кроме того, здесь Wolfram Alpha выводит таблицу для сравнения погрешностей всех численных методов, которые использует система (в крайней точке интервала интегрирования дифференциального уравнения):

В рассмотренном примере шаг интегрирования, равный 0.2, был выбран автоматически. Выше было сказано, что можно явно указать нужный шаг интегрирования. Причем, нужно выбирать его так, чтобы на заданном отрезке умещалось не менее, чем 10 шагов интегрирования. Уменьшая шаг интегрирования, можно получать численные решения с желаемой точностью точностью:
solve {y'+2xy=0, y(1)=2} Euler method h=.05 x=1..3

Численные решения дифференциальных уравнений, рассмотренные выше, были получены простейшим методом - методом Эйлера (Euler method). Как мы видели выше, Wolfram Alpha реализует и другие численные методы интегрирования дифференциальных уравнений. Посмотрите примеры (по ссылке):
- Euler method - метод Эйлера;
- midpoint method - метод средних точек, модифицированный метод Эйлера;
- Heun's method (метод Хойна, вариант модифицированного метода Эйлера)
- third‐order Runge‐Kutta method (метод Рунге-Кутты третьего порядка)
- fourth‐order Runge‐Kutta method (метод Рунге-Кутты четвертого порядка)
- Runge‐Kutta‐Fehlberg method (метод Рунге-Кутты-Фелберга, RKF method )
- Bogacki‐Shampine method
- Dormand‐Prince method (DOPRI method)
- backward Euler method
- implicit midpoint method
solve {y```= -2xy`, y(0) = 0, y`(0) = -1, y``(0) = -2} Runge-Kutta method h =.25 x=0..3

Таким образом, численное решение обыкновенных дифференциальных уравнений в системе Wolfram Alpha является достаточно простой стандартной процедурой, соблюдение которой гарантирует правильный результат.
