Как найти вероятность попадания случайной величины в заданный интервал? Это одна из самых известных и простейших задач теории вероятностей, которая в Wolfram|Alpha решается довольно просто.
Вероятность попадания случайной величины X в числовой интервал (a; b) с помощью математической символики записывается следующим образом:

Эта вероятность зависит от того, какое распределение вероятностей имеет данная случайная величина. Это важно понимать, и обязательно нужно учитывать при вычислениях.
Вузовские пособия и курсы по высшей математике и теории вероятностей чаще всего подробно рассматривают вопрос о вычислении вероятности попадания в заданный интервал, лишь для нормально распределенной случайной величины, а также для дискретных случайных величин, которые имеют биномиальное распределение вероятностей. Потому-то о том, как искать вероятность попадания случайной величины X в заданный интервал, когда она имеет какое-либо иное распределение вероятностей, большинство студентов имеет лишь отдаленное представление.
Однако же, в курсах математического моделирования, в технических, экономических дисциплинах возникает необходимость вновь обращаться к этой задаче. Причем, здесь нельзя ограничиться только лишь нормальным или биномиальным распределением вероятностей.
Как найти вероятность попадания в заданный интервал для любой случайной величины? Ответ на этот вопрос также даст Wolfram|Alpha. Достаточно лишь ввести систему соответствующий запрос на вычисление вероятности. При этом нужно указать распределение случайной величины и параметры этого распределения.
Например, чтобы найти вероятность попадания непрерывной случайной величины X, которая имеет нормальное распределение с параметрами (математическое ожидание) mean=1 и (средне-квадратическое отклонение) sd=2 в интервал (-1.2; 2.3) используется такой запрос:
P(-1.2<X<2.3) X~normal mean=1 sd=2

Как видите, здесь Wolfram|Alpha не только выводит числовой результат - значение искомой вероятности, равное 0,606488, но также и его графическую интерпретацию: на графике плотности нормального распределения обозначена фигура (криволинейная трапеция), площадь которой равна искомой вероятности 0,606488. Это соответствует известной формуле:

где f(x) - плотность вероятности нормального распределения (pdf NormalDistribution[mean, sd]). Иначе говоря, для непрерывных случайных величин тот же самый результат можно было бы получить путем интегрирования.
Однако, соответствующий запрос, с которым естественно было обратиться к системе Wolfram|Alpha, к сожалению, не дает того результата, который ожидаешь. Посмотрите сами:
integrate pdf NormalDistribution[1, 2], x=-1.2..2.3
Поэтому, чтобы получить нужный результат путем интегрирования, придется вручную ввести подынтегральную функцию - плотность вероятности нормального распределения с заданными параметрами mean=1 и sd=2. В результате, естественно, получим ответ, который совпадает с предыдущим:
integrate (e^((-(x-1)^2)/8)/(2 sqrt(2 π)), x=-1.2..2.3

Последний запрос можно также сформулировать несколько иначе. Результат будет представлен несколько в ином виде, но сам результат, конечно, будет тот же самый:
P(-1.2<X<2.3) = integrate (e^((-(x-1)^2)/8)/(2 sqrt(2 π)), x=-1.2..2.3

Имеется еще один способ, как проверить полученные выше результаты. А именно: можно воспользоваться формулой для вычисления вероятности попадания случайной величины в заданный интервал, которая использует функцию распределения вероятностей:

Здесь: F(x) - функция плотности нормального распределения cdf normal distribution mean=1 sd=2. Далее подробности использования этого способа в Wolfram|Alpha не приводятся, поскольку он на поверку оказывается самым неудобным для практического использования.
Посмотрим теперь, как в Wolfram|Alpha решается поставленная в заголовке поста задача про вероятность попадания случайной величины в заданный интервал для других случайных величин, которые имеют распределения вероятностей отличные от нормального. При этом будем в качестве основного способа использовать запрос вида P(a<X<b) [распределение] [параметры].
Для величины, имеющей t-распределение Стьюдента с 12 степенями свободы получим:
P[-1.2<X<2.3] X~student t dof=12
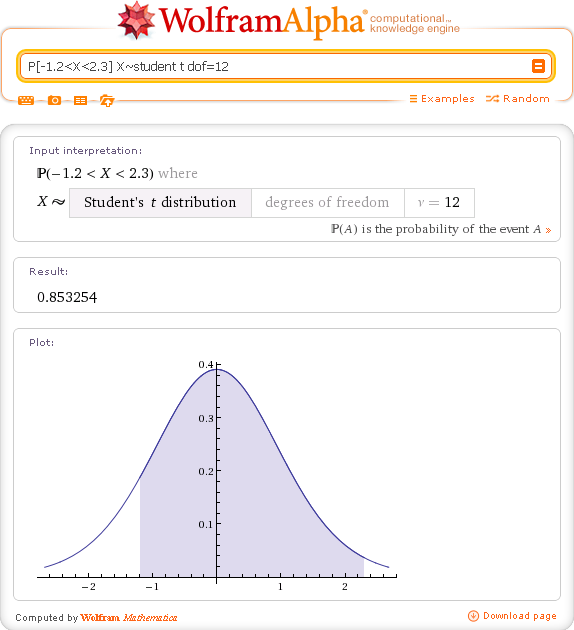
Для распределения хи-квадрат с 9-ю степенями свободы:
P(-1.2<X<2.3) X~chi-square dof=9
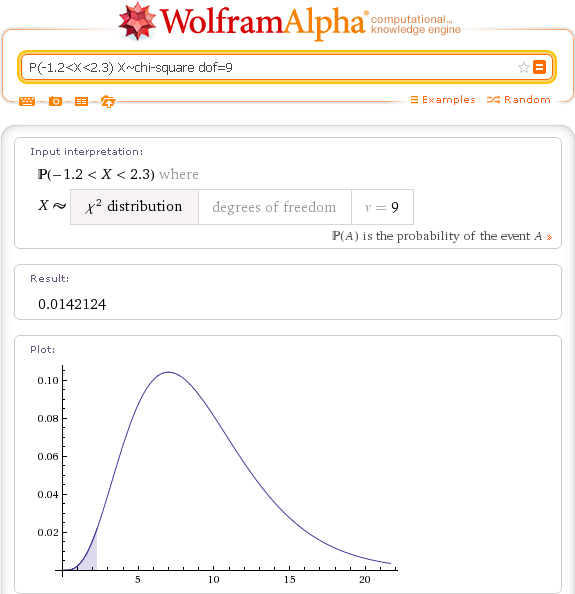
Аналогичный результат также дают запросы на "естественном языке". Посмотрите такие примеры:
x chi-square with 9 dof, probabiality 3x-5<7
probabiality 3x-5<7 where x chi-square with 9 dof
P(3x-5<7) where x chi-square with 9 dof
P(3x-5<7), x chi-square with 9 dof
P(3x-5<7) x chi-square dof 9
Еще один пример. Для распределения Рэлея с параметром scale=3 получаем:
P(1.5<X<4.7) X~rayleigh distribution scale=3
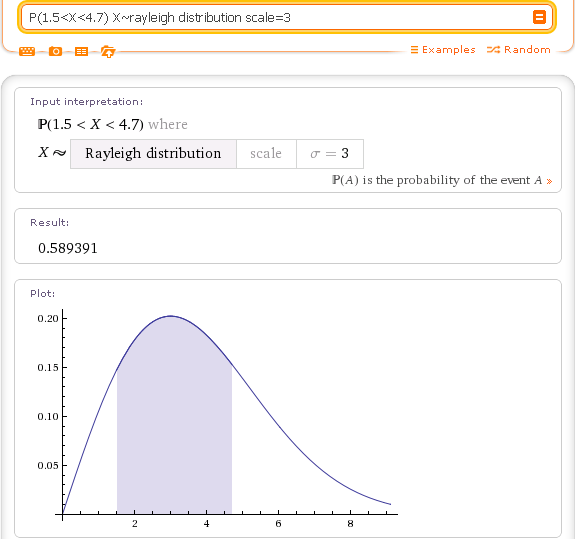
Пример для дискретного распределения. Распределение Пуассона с параметром mean=5
P(1.5<X<4.7) X~poisson distribution mean=5

Надеюсь, что выше сказано уже достаточно, чтобы Вы смогли с помощью Wolfram|Alpha самостоятельно вычислить вероятность попадания любой случайной величины в любой заданный интервал.
Конечно, Вам нужно будет получить информацию о названиях других вероятностных распределений случайных величин и их параметрах. Подробности об этом Вы найдете в предыдущих постах Непрерывные вероятностные распределения в Wolfram|Alpha и Дискретные вероятностные распределения в Wolfram|Alpha.
P. S.
Есть также еще один способ вычисления вероятности попадания случайной величины в заданный интервал - использование калькуляторов вероятностей. Но об этом будет отдельный пост.
Вероятность попадания случайной величины X в числовой интервал (a; b) с помощью математической символики записывается следующим образом:

Эта вероятность зависит от того, какое распределение вероятностей имеет данная случайная величина. Это важно понимать, и обязательно нужно учитывать при вычислениях.
Вузовские пособия и курсы по высшей математике и теории вероятностей чаще всего подробно рассматривают вопрос о вычислении вероятности попадания в заданный интервал, лишь для нормально распределенной случайной величины, а также для дискретных случайных величин, которые имеют биномиальное распределение вероятностей. Потому-то о том, как искать вероятность попадания случайной величины X в заданный интервал, когда она имеет какое-либо иное распределение вероятностей, большинство студентов имеет лишь отдаленное представление.
Однако же, в курсах математического моделирования, в технических, экономических дисциплинах возникает необходимость вновь обращаться к этой задаче. Причем, здесь нельзя ограничиться только лишь нормальным или биномиальным распределением вероятностей.
Как найти вероятность попадания в заданный интервал для любой случайной величины? Ответ на этот вопрос также даст Wolfram|Alpha. Достаточно лишь ввести систему соответствующий запрос на вычисление вероятности. При этом нужно указать распределение случайной величины и параметры этого распределения.
Например, чтобы найти вероятность попадания непрерывной случайной величины X, которая имеет нормальное распределение с параметрами (математическое ожидание) mean=1 и (средне-квадратическое отклонение) sd=2 в интервал (-1.2; 2.3) используется такой запрос:
P(-1.2<X<2.3) X~normal mean=1 sd=2

Как видите, здесь Wolfram|Alpha не только выводит числовой результат - значение искомой вероятности, равное 0,606488, но также и его графическую интерпретацию: на графике плотности нормального распределения обозначена фигура (криволинейная трапеция), площадь которой равна искомой вероятности 0,606488. Это соответствует известной формуле:

где f(x) - плотность вероятности нормального распределения (pdf NormalDistribution[mean, sd]). Иначе говоря, для непрерывных случайных величин тот же самый результат можно было бы получить путем интегрирования.
Однако, соответствующий запрос, с которым естественно было обратиться к системе Wolfram|Alpha, к сожалению, не дает того результата, который ожидаешь. Посмотрите сами:
integrate pdf NormalDistribution[1, 2], x=-1.2..2.3
Поэтому, чтобы получить нужный результат путем интегрирования, придется вручную ввести подынтегральную функцию - плотность вероятности нормального распределения с заданными параметрами mean=1 и sd=2. В результате, естественно, получим ответ, который совпадает с предыдущим:
integrate (e^((-(x-1)^2)/8)/(2 sqrt(2 π)), x=-1.2..2.3

Последний запрос можно также сформулировать несколько иначе. Результат будет представлен несколько в ином виде, но сам результат, конечно, будет тот же самый:
P(-1.2<X<2.3) = integrate (e^((-(x-1)^2)/8)/(2 sqrt(2 π)), x=-1.2..2.3

Имеется еще один способ, как проверить полученные выше результаты. А именно: можно воспользоваться формулой для вычисления вероятности попадания случайной величины в заданный интервал, которая использует функцию распределения вероятностей:

Здесь: F(x) - функция плотности нормального распределения cdf normal distribution mean=1 sd=2. Далее подробности использования этого способа в Wolfram|Alpha не приводятся, поскольку он на поверку оказывается самым неудобным для практического использования.
Посмотрим теперь, как в Wolfram|Alpha решается поставленная в заголовке поста задача про вероятность попадания случайной величины в заданный интервал для других случайных величин, которые имеют распределения вероятностей отличные от нормального. При этом будем в качестве основного способа использовать запрос вида P(a<X<b) [распределение] [параметры].
Для величины, имеющей t-распределение Стьюдента с 12 степенями свободы получим:
P[-1.2<X<2.3] X~student t dof=12

Для распределения хи-квадрат с 9-ю степенями свободы:
P(-1.2<X<2.3) X~chi-square dof=9

Аналогичный результат также дают запросы на "естественном языке". Посмотрите такие примеры:
x chi-square with 9 dof, probabiality 3x-5<7
probabiality 3x-5<7 where x chi-square with 9 dof
P(3x-5<7) where x chi-square with 9 dof
P(3x-5<7), x chi-square with 9 dof
P(3x-5<7) x chi-square dof 9
Еще один пример. Для распределения Рэлея с параметром scale=3 получаем:
P(1.5<X<4.7) X~rayleigh distribution scale=3

Пример для дискретного распределения. Распределение Пуассона с параметром mean=5
P(1.5<X<4.7) X~poisson distribution mean=5

Надеюсь, что выше сказано уже достаточно, чтобы Вы смогли с помощью Wolfram|Alpha самостоятельно вычислить вероятность попадания любой случайной величины в любой заданный интервал.
Конечно, Вам нужно будет получить информацию о названиях других вероятностных распределений случайных величин и их параметрах. Подробности об этом Вы найдете в предыдущих постах Непрерывные вероятностные распределения в Wolfram|Alpha и Дискретные вероятностные распределения в Wolfram|Alpha.
P. S.
Есть также еще один способ вычисления вероятности попадания случайной величины в заданный интервал - использование калькуляторов вероятностей. Но об этом будет отдельный пост.