Надеюсь, вы уже установили расширение, тулбар или плагин Wolfram|Alpha для вашего браузера, как это было сказано в предыдущем посте. Сделайте это, чтобы вам было удобнее использовать Wolfram Alpha, и продолжим.
Для решения уравнений и их систем в Wolfram|Alpha используется запрос solve
Вот запрос, который означает: "Решить систему линейных уравнений":
solve x+y+z-u=1, 2x+y+z-2u=1, x+y+2z+u=1, x+y+2z+4u=2

Другой вариант (без использования solve), который также позволяет получить решение системы: достаточно просто ввести уравнения системы через запятую.
x+y+z-u=1, 2x+y+z-2u=1, x+y+2z+u=1, x+y+2z+4u=2
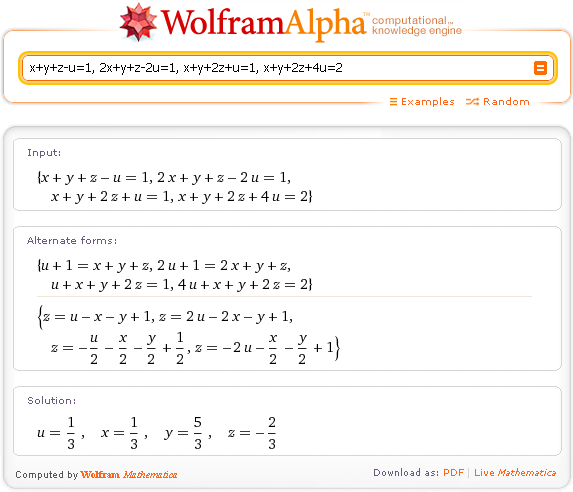
Wolfam Alpha решает не только определенные, но и неопределенные системы линейных алгебраических уравнений. Вот пример, где переменных на одну больше, чем уравнений (без solve):
x+y+z-u=1, 2x+y+z-2u=1, x+y+2z+u=1

То же самое, но с использованием запроса solve:
solve x+y+z-u=1, 2x+y+z-2u=1, x+y+2z+u=1
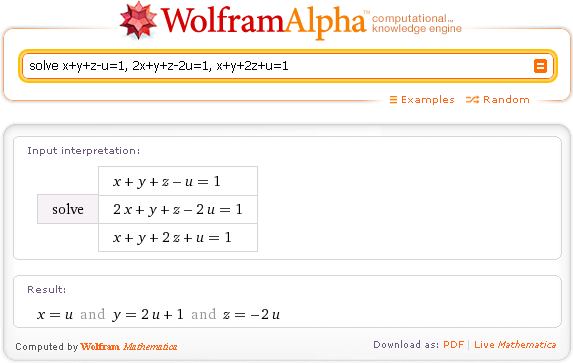
Wolfram Alpha также позволяет решать системы линейных алгебраических уравнений в матричном виде. Об этом будет следующий пост на эту тему.
Для решения уравнений и их систем в Wolfram|Alpha используется запрос solve
Вот запрос, который означает: "Решить систему линейных уравнений":
solve x+y+z-u=1, 2x+y+z-2u=1, x+y+2z+u=1, x+y+2z+4u=2

Другой вариант (без использования solve), который также позволяет получить решение системы: достаточно просто ввести уравнения системы через запятую.
x+y+z-u=1, 2x+y+z-2u=1, x+y+2z+u=1, x+y+2z+4u=2

Wolfam Alpha решает не только определенные, но и неопределенные системы линейных алгебраических уравнений. Вот пример, где переменных на одну больше, чем уравнений (без solve):
x+y+z-u=1, 2x+y+z-2u=1, x+y+2z+u=1

То же самое, но с использованием запроса solve:
solve x+y+z-u=1, 2x+y+z-2u=1, x+y+2z+u=1

Wolfram Alpha также позволяет решать системы линейных алгебраических уравнений в матричном виде. Об этом будет следующий пост на эту тему.